300 pnl. vo svojej práci Elements delí Euklid úsečku v bode 0,618
na jej extrém a stredovú hodnotu a prichádza s prvou jasnou definíciou
(čísla dnes známeho ako) Phi.
Tento výrok podnecuje vznik termínu zlatý priemer.
360 pnl. Platón v práci Timaeus: (číslo dnes známe ako) Phi
je najčastejším vo všetkých matematických vzťahoch a je kľúčom k fyzike vesmíru.
560 pnl. ešte pred ním Pytagoras objaví (číslo dnes známe ako) Phi pomocou zvuku.
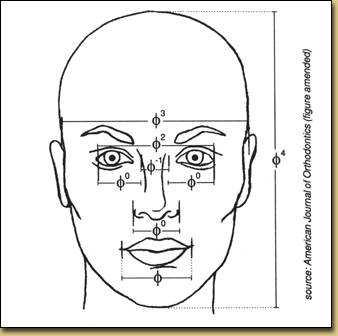
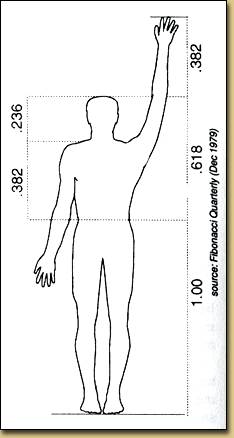
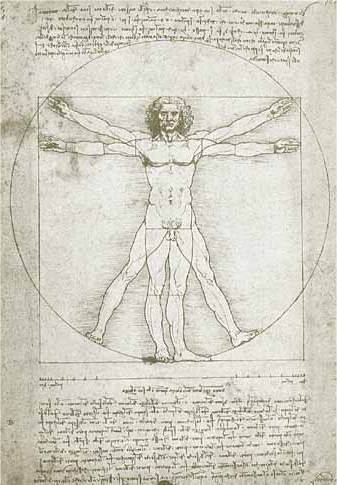
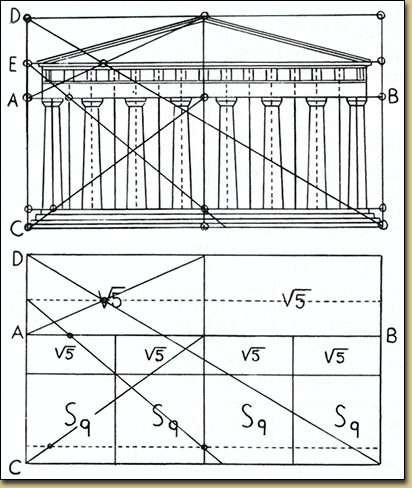Gréci nachádzajú phi v prírode, v štruktúre ulít, veľkosti listov,
konárových vzorcoch stromov a stavbe ľudského tela.
veria, že číslo opisuje rozmery priemerných, a teda "ideálnych" telesných čŕt,
ako tváre, torza, a proporcií rúk a nôh k veľkosti tela.
Phi sa považuje za priaznivé a esteticky príjemné
a používa sa v tvorbe aj mimo prírody
ako pomôcka pre verné zobrazovanie človeka v maľbe a soche,
tiež vo filozofii, paidei a v architektúre budov (viď Pantheon) a dvorov.
ešte hlboko pred Grékmi použijú Phi Egypťania pri stavbe Veľkej pyramídy v Gize.
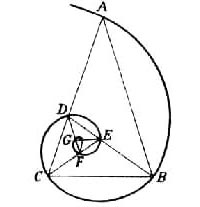
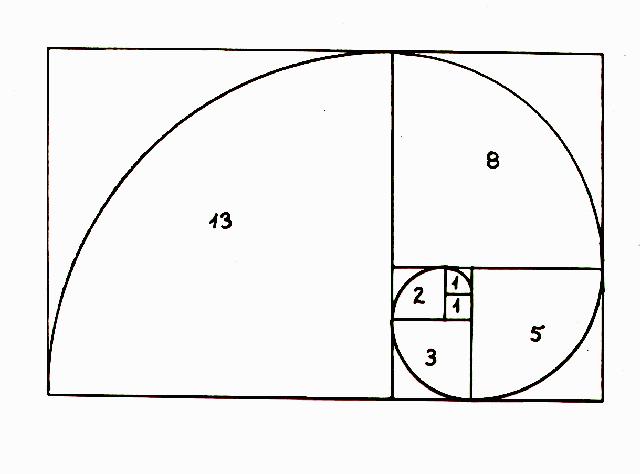v roku 1200 Fibonacci objaví číselnú radu úzko súvisiacu so zlatým rezom.
na jej vygenerovanie použije príklad množenia zajacov.
to describe the growth of a hypothetical rabbit population.
The numbers describe the number of pairs in a (somewhat idealized) rabbit population after
n months if it is assumed that
* the first month there is just one newly born pair,
* newly born pairs become productive from their second month on,
* we have no genetic problems whatsoever generated by inbreeding,
* each month every productive pair begets a new pair, and
* the rabbits never die
Fibonacciho rada:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597,
2584, 4181, 6765, 10946...
krásny príklad na algoritmus, ukážme si ho použitím pseudokódu.
n = 1
n_minuly_mesiac = 0
repeat
write n
novonarodene = n_minuly_mesiac
n_minuly_mesiac = n
n = n + novonarodene
until false
simulácia priebehu algoritmu bude potom vyzerať takto:
n n_minuly_mesiac (novonarodene) vystup
1 0 1
1 1 (0) 1
2 1 (1) 2
3 2 (1) 3
5 3 (2) 5
..
Okrem phi poznáme dokonca aj iné spojenie Fibonacciho s Euklidom.
Euklidov algoritmus je jeden z najstarších algoritmov.
počíta najvyšší spoločný deliteľ dvoch čísel.
Euklidov algoritmus kalkuluje výsledok najdlhšie pre dve po sebe idúce čísla Fibonacciho rady.
po Fibonaccim zažíva fenomén zlatého rezu svoju renesanciu počas renesancie.
v 1495 Leonardo da Vinci použije zlatý rez na definíciu všetkých základných
proporcií svojej maľby Posledná večera, od rozmerov stola, pri ktorom sedí
Kristus so svojimi učeníkmi, po rozmery stien a okien v pozadí.
Proporcia je široko používaná renesančnými umelcami v maľbách a sochách
na dosiahnutie balansu a krásy.
v 1509 Leonardo da Vinci vytvára ilustráciu piatich Platónovských telies
pre dizertačnú prácu Luca Pacioliho De Divina Proportione.
Nazýva ju "sectio aurea," čo v latinčine znamená zlatý rez.
phi možno nájsť na ulitách, v tvare baraních rohov, mlieka v káve,
odtlačkov prstov, či Mliečnej dráhy.
na základe zlatého rezu je tiež skonštruovaný pentagram.
v zlatom reze je preťaný kresťanský kríž.
Fibonacciho špirála, resp. zlatý rez, či zlatý priemer, resp. phi
dnes na nás pozerá z architektúry, dizajnu, hudby, sôch.
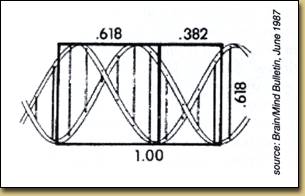ideálnu proporciu nachádzame aj v DNA.
TRANSLAB[4]: V. KÓD V GENETIKE (powerpoint 7mb)TRANSLAB[4]: VI. RANÁ POČÍTAČOVÁ VIZUÁLNA ESTETIKA (HTML verzia)